Joint work with Matteo Gallet, Georg Grasegger and Josef Schicho
In the paper Combinatorics of Bricard’s octahedra, we give a new proof for the classification of Bricard’s octahedra. Our technique mixes elementary facts on metric geometry (in particular, properties of quadrilaterals on the sphere) and the results from our previous work On the existence of paradoxical motions of generically rigid graphs on the sphere, which are based on a construction in algebraic geometry (the moduli space of rational stable curves with marked points).
In the paper Zero-sum cycles in flexible polyhedra we give a generalization of one of the key results used to classify Bricard’s octahedra using another technique. Namely, we show that for a flexible polyhedron there exists a cycle of edges whose edge lengths sum up to zero once they are suitable signed.
Here we provide animations for the motions of each of the three families of flexible octahedra.
Type I
Octahedra whose vertices form three pairs of points symmetric with respect to a line.

Type II
Octahedra whose vertices are given by two pairs of points symmetric with respect to a plane passing through the last two vertices.
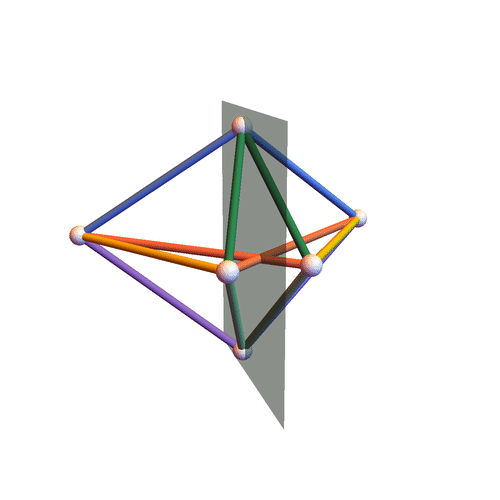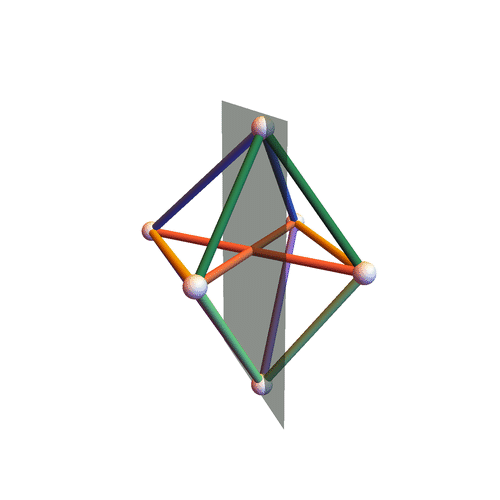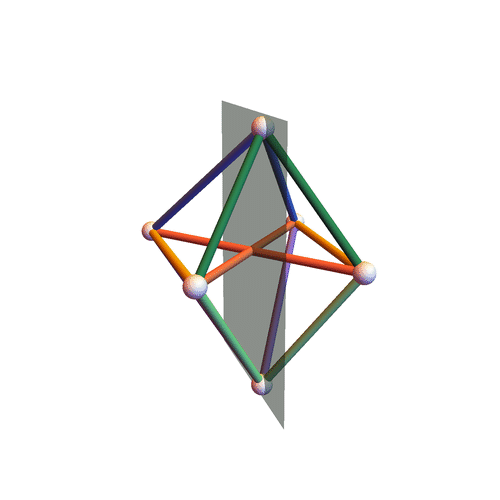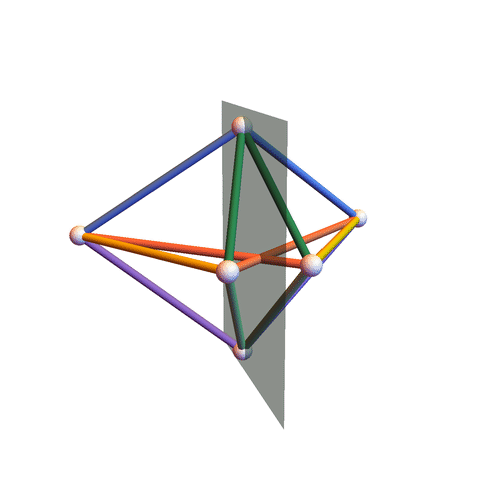
Type III
Octahedra all of whose pyramids (here by “pyramid” we mean a $4$-tuple of edges sharing a vertex) have the following property: the two pairs of opposite angles (here by “angle” of a pyramid we mean the angle formed by two concurrent edges belonging to the same face) are constituted of angles that are either both equal or both supplementary; moreover, we ask the lengths $\ell_{ij}$ of the edges (the vertices of the octahedron are labeled by the numbers ${1, \dotsc, 6}$) to satisfy three linear equations of the form:
$$\eta_{35} \, \ell_{35} + \eta_{45} \, \ell_{45} + \eta_{46} \, \ell_{46} + \eta_{36} \, \ell_{36} = 0$$ $$\eta_{14} \, \ell_{14} + \eta_{24} \, \ell_{24} + \eta_{23} \, \ell_{23} + \eta_{13} \, \ell_{13} = 0$$ $$\eta_{15} \, \ell_{15} + \eta_{25} \, \ell_{25} + \eta_{26} \, \ell_{26} + \eta_{16} \, \ell_{16} = 0$$
where $\eta_{ij} \in \{1,-1\}$ and in each equation we have exactly two positive $\eta_{ij}$ and two negative ones.
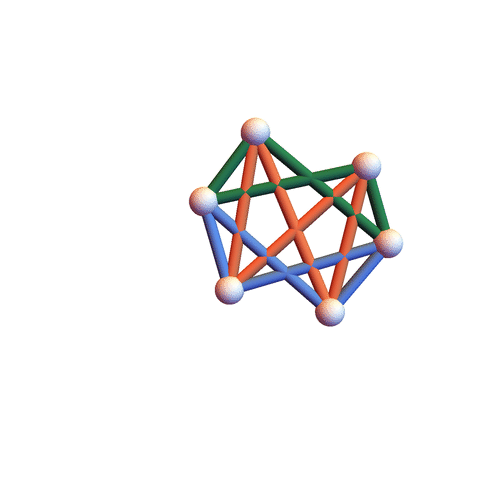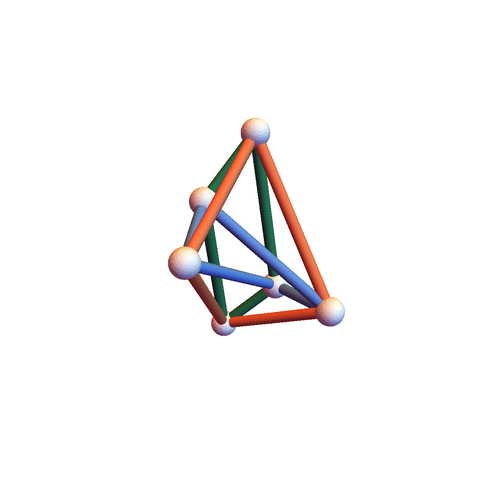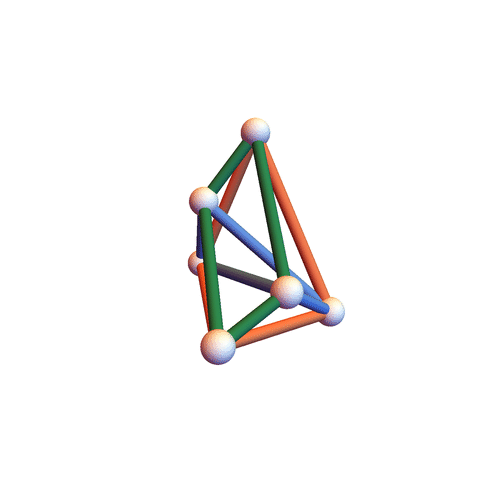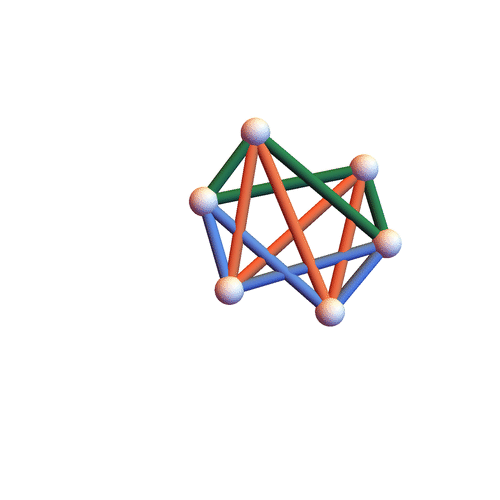
Type I&II&III
The three families have non-empty intersection – the motion below is of all three types.