NAC-colorings

This class implements a NAC-coloring of a graph.

A coloring of edges $\delta\colon E_G\rightarrow \{\text{blue, red}\}$ is called a NAC-coloring, if it is surjective and for every cycle $C$ in $G$, either all edges of $C$ have the same color, or $C$ contains at least 2 edges in each color [GLS2018].

Methods

NAC2int()	Return the integer representation of the NAC-coloring.
blue_components()	NO DOCSTRING
blue_edges()	Return the list of blue edges of the NAC-coloring.
blue_subgraph()	NO DOCSTRING
color()	Return the color of an edge.
conjugated()	Return the conjugated NAC-coloring.
cycle_has_orthogonal_diagonals()	Return if the NAC-coloring implies orthogonal diagonals for a given 4-cycle.
grid_coordinates()	Return coordinates for the grid construction. The optional parameters ordered_red, ordered_blue can be used to specify the order of components to be taken.
grid_coordinates_are_injective()	Return if the grid coordinates are injective.
is_NAC_coloring()	Return if the coloring is a NAC-coloring.
is_blue()	Return if the edge is blue.
is_equal()	Return if the NAC-coloring is equal to other_coloring.
is_isomorphic()	Return if the NAC-coloring is isomorphic to other_coloring.
is_red()	Return if the edge is red.
is_singleton()	Return if the NAC-coloring is a singleton.
isomorphic_NAC_coloring()	Return the NAC-coloring under a morphism sigma.
name()	Return the name of the NAC-coloring.
path_is_unicolor()	Return if the edges of the path have the same color.
plot()	Return a plot of the NAC-coloring.
print_tikz()	Print TikZ code for the graph colored with the NAC-coloring.
red_components()	NO DOCSTRING
red_edges()	Return the list of red edges of the NAC-coloring.
red_subgraph()	NO DOCSTRING
set_name()	Set a new name.

AUTHORS:

• Jan Legerský (2019-01-15): initial version
• Jan Legerský (2020-03-12): update to SageMath 9.0

NACcoloring

class flexrilog.NAC_coloring.NACcoloring(G, coloring, name=None, check=True)

Bases: sage.structure.sage_object.SageObject

The class for a NAC-coloring of a graph.

A coloring of edges $\delta\colon E_G\rightarrow \{\text{blue, red}\}$ is called a NAC-coloring, if it is surjective and for every cycle $C$ in $G$, either all edges of $C$ have the same color, or $C$ contains at least 2 edges in each color [GLS2018].

INPUT:

• G – a graph of type FlexRiGraph to which the NAC-coloring belongs.
• coloring – a dictionary assigning to every edge of G either "red" or "blue", or a list consisting of two lists giving a partition of the edges of G
• name – an optional name of the NAC-coloring
• check – if True (default), then surjectivity and the cycle conditions are checked. (see is_NAC_coloring()). A ValueError is raised if the check fails

EXAMPLES:

sage: from flexrilog import NACcoloring
sage: from flexrilog import GraphGenerator
sage: G = GraphGenerator.SmallestFlexibleLamanGraph(); G
SmallestFlexibleLamanGraph: FlexRiGraph with the vertices [0, 1, 2, 3, 4] and edges [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 4), (3, 4)]
sage: delta = NACcoloring(G,[[(0, 1), (0, 2), (0, 3), (1, 2), (1, 3)], [(2, 4), (3, 4)]]); delta
NAC-coloring with red edges [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3]] and blue edges [[2, 4], [3, 4]]

By default, it is checked whether the coloring is a NAC-coloring:

sage: delta = NACcoloring(G,[[(0, 1), (0, 2)], [(0, 3), (1, 2), (1, 3), (2, 4), (3, 4)]]); delta
Traceback (most recent call last):
...
ValueError: The coloring is not a NAC-coloring.
sage: delta = NACcoloring(G,[[(0, 1), (0, 2)], [(0, 3), (1, 2), (1, 3), (2, 4), (3, 4)]], check=False); delta
NAC-coloring with red edges [[0, 1], [0, 2]] and blue edges [[0, 3], [1, 2], [1, 3], [2, 4], [3, 4]]
sage: delta.is_NAC_coloring()
False

A dictionary can be also used as an input:

sage: delta = NACcoloring(G,{(0, 1) : "red", (0, 2) : "red", (0, 3) : "red", (1, 2) : "red", (1, 3) : "red", (2, 4) : "blue", (3, 4) : "blue"}); delta
NAC-coloring with red edges [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3]] and blue edges [[2, 4], [3, 4]]

The coloring must be a partition of edges of G:

sage: delta = NACcoloring(G,[[(0, 1), (0, 2), (0, 3), (1, 3)], [(2, 4), (3, 4)]]); delta
Traceback (most recent call last):
...
RuntimeError: The edges of the NAC-coloring do not match the edges of the graph.

NAC2int()

Return the integer representation of the NAC-coloring.

The binary representation of the number is obtained by sorting the edges lexicographically and setting 1 for red edges, 0 for blue edges, or the other way around if the first edge is blue.

EXAMPLE:

sage: from flexrilog import GraphGenerator
sage: delta = GraphGenerator.Q1Graph().NAC_colorings()[0]
sage: delta.NAC2int()
3871
sage: 3871.binary()
'111100011111'

blue_components()

blue_edges()

Return the list of blue edges of the NAC-coloring.

blue_subgraph()

color(u, v=None)

Return the color of an edge.

INPUT:

If v is None, then u is consider to be an edge. Otherwise, uv is taken as the edge.

EXAMPLES:

sage: from flexrilog import FlexRiGraph
sage: G = FlexRiGraph(graphs.CompleteBipartiteGraph(3,3))
sage: delta = G.NAC_colorings()[0]
sage: delta.color(0,3)
'red'
sage: delta.color([2,4])
'blue'
sage: delta.color(1,2)
Traceback (most recent call last):
...
ValueError: There is no edge [1, 2]

conjugated()

Return the conjugated NAC-coloring.

cycle_has_orthogonal_diagonals(cycle)

Return if the NAC-coloring implies orthogonal diagonals for a given 4-cycle.

EXAMPLE:

sage: from flexrilog import GraphGenerator
sage: K33 = GraphGenerator.K33Graph()
sage: [[delta.name(), [cycle for cycle in K33.four_cycles() if delta.cycle_has_orthogonal_diagonals(cycle)]] for delta in K33.NAC_colorings()]
[['omega5', []],
 ['omega3', []],
 ['omega1', []],
 ['omega6', []],
 ['epsilon56', [(1, 2, 3, 4)]],
 ['epsilon36', [(1, 2, 5, 4)]],
 ['epsilon16', [(2, 3, 4, 5)]],
 ['omega4', []],
 ['epsilon45', [(1, 2, 3, 6)]],
 ['epsilon34', [(1, 2, 5, 6)]],
 ['epsilon14', [(2, 3, 6, 5)]],
 ['omega2', []],
 ['epsilon25', [(1, 4, 3, 6)]],
 ['epsilon23', [(1, 4, 5, 6)]],
 ['epsilon12', [(3, 4, 5, 6)]]]

grid_coordinates(ordered_red=[], ordered_blue=[])

Return coordinates for the grid construction.

The optional parameters ordered_red, ordered_blue can be used to specify the order of components to be taken.

See [GLS2018] for the description of the grid construction.

TODO:

test

grid_coordinates_are_injective()

Return if the grid coordinates are injective.

EXAMPLES:

sage: from flexrilog import GraphGenerator
sage: G = GraphGenerator.ThreePrismGraph()
sage: delta = G.NAC_colorings()[0]
sage: delta.grid_coordinates_are_injective()
True

sage: from flexrilog import GraphGenerator
sage: G = GraphGenerator.SmallestFlexibleLamanGraph()
sage: delta = G.NAC_colorings()[0]
sage: delta.grid_coordinates_are_injective()
False

is_NAC_coloring()

Return if the coloring is a NAC-coloring.

The implementation uses Lemma 2.4 in [GLS2018].

EXAMPLES:

sage: from flexrilog import NACcoloring, GraphGenerator
sage: G = GraphGenerator.SmallestFlexibleLamanGraph(); G
SmallestFlexibleLamanGraph: FlexRiGraph with the vertices [0, 1, 2, 3, 4] and edges [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 4), (3, 4)]
sage: delta = NACcoloring(G,[[(0, 1), (0, 2), (0, 3), (1, 2), (1, 3)], [(2, 4), (3, 4)]], check=False)
sage: delta.is_NAC_coloring()
True

NAC-coloring must be surjective:

sage: delta = NACcoloring(G,[[], [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 4), (3, 4)]], check=False)
sage: delta.is_NAC_coloring()
False

And it has to satisfy the cycle conditions:

sage: delta = NACcoloring(G,[[(0, 1), (0, 2)], [(0, 3), (1, 2), (1, 3), (2, 4), (3, 4)]], check=False)
sage: delta.is_NAC_coloring()
False

is_blue(u, v=None)

Return if the edge is blue.

INPUT:

If v is None, then u is consider to be an edge. Otherwise, uv is taken as the edge.

EXAMPLES:

sage: from flexrilog import FlexRiGraph
sage: G = FlexRiGraph(graphs.CompleteBipartiteGraph(3,3))
sage: delta = G.NAC_colorings()[0]
sage: delta.is_blue(2,4)
True
sage: delta.is_blue([0,4])
False
sage: delta.is_blue(1,2)
Traceback (most recent call last):
...
ValueError: There is no edge [1, 2]

is_equal(other_coloring, moduloConjugation=True)

Return if the NAC-coloring is equal to other_coloring.

INPUT:

• moduloConjugation – If True (default), then the NAC-colorings are compared modulo swapping colors.

EXAMPLES:

sage: from flexrilog import NACcoloring, GraphGenerator
sage: G = GraphGenerator.SmallestFlexibleLamanGraph(); G
SmallestFlexibleLamanGraph: FlexRiGraph with the vertices [0, 1, 2, 3, 4] and edges [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 4), (3, 4)]
sage: delta1 = NACcoloring(G,[[(0, 1), (0, 2), (0, 3), (1, 2), (1, 3)], [(2, 4), (3, 4)]])
sage: delta2 = NACcoloring(G,[[(2, 4), (3, 4)],[(0, 1), (0, 2), (0, 3), (1, 2), (1, 3)]])
sage: delta1.is_equal(delta2)
True
sage: delta1.is_equal(delta2, moduloConjugation=False)
False

is_isomorphic(other_coloring, check=True, certificate=False, aut_group=None)

Return if the NAC-coloring is isomorphic to other_coloring.

NAC-colorings $\delta_1$ and $\delta_2$ of a graph $G$ are isomorphic if and only if there exists and automorphism $\sigma$ of $G$ such that

• $\delta_1(uv) = \text{red} \iff \delta_2(\sigma(u),\sigma(v)) = \text{red}$ for all $uv\in E_G$, or
• $\delta_1(uv) = \text{blue} \iff \delta_2(\sigma(u),\sigma(v)) = \text{red}$ for all $uv\in E_G$.

INPUT:

• other_coloring – a NAC-colorings that is checked to be isomorphic with this NAC-coloring.
• check – if True (default), then it is checked whether the NAC-colorings belong to the same graph.
• certificate – if False (default), then only boolean is returned. Otherwise, (True, sigma) resp. (false, None) is returned, where sigma is the graph automorphism mapping the NAC-coloring to the other_coloring.

EXAMPLES:

sage: from flexrilog import FlexRiGraph, NACcoloring
sage: G = FlexRiGraph(graphs.CompleteBipartiteGraph(3,3))
sage: colorings = G.NAC_colorings()
sage: col1, col2, col3 = colorings[4], colorings[5], colorings[7]
sage: col1
NAC-coloring with red edges [[0, 3], [0, 4], [1, 3], [1, 4], [2, 5]] and blue edges [[0, 5], [1, 5], [2, 3], [2, 4]]
sage: col2
NAC-coloring with red edges [[0, 3], [0, 4], [1, 5], [2, 3], [2, 4]] and blue edges [[0, 5], [1, 3], [1, 4], [2, 5]]
sage: col3
NAC-coloring with red edges [[0, 3], [0, 5], [1, 3], [1, 5], [2, 3], [2, 5]] and blue edges [[0, 4], [1, 4], [2, 4]]
sage: col1.is_isomorphic(col2)
True
sage: _, sigma = col1.is_isomorphic(col2, certificate=True); sigma
(0,2,1)
sage: col1.isomorphic_NAC_coloring(sigma).is_equal(col2)
True
sage: col1.is_isomorphic(col3)
False

col1: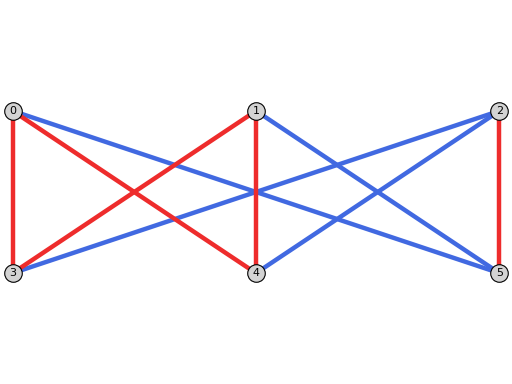

col2: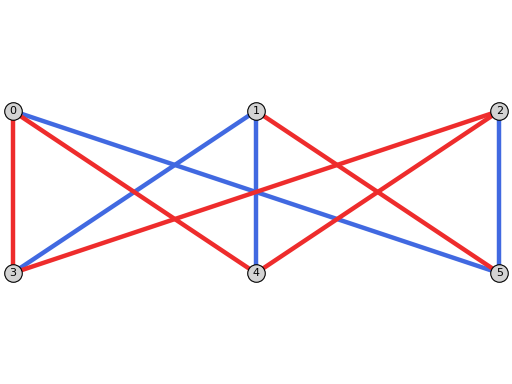

is_red(u, v=None)

Return if the edge is red.

INPUT:

If v is None, then u is consider to be an edge. Otherwise, uv is taken as the edge.

EXAMPLES:

sage: from flexrilog import FlexRiGraph
sage: G = FlexRiGraph(graphs.CompleteBipartiteGraph(3,3))
sage: delta = G.NAC_colorings()[0]
sage: delta.is_red(0,3)
True
sage: delta.is_red([2,4])
False
sage: delta.is_red(1,2)
Traceback (most recent call last):
...
ValueError: There is no edge [1, 2]

is_singleton(NACs=[])

Return if the NAC-coloring is a singleton.

Let $G$ be a graph and $N$ be a subset of its NAC-colorings. A NAC-coloring $\delta$ is called singleton w.r.t.$N$ if $|\{(\delta(e),\delta’(e))\colon e\in E_{Q_1}\}|\,\neq 3$ for all $\delta’\in N$.

INPUT:

• NACs – being singleton is considered w.r.t the list of NAC-colorings NACs. If this is empty (default), then all NAC-colorings of the graph are considered.

EXAMPLES:

sage: from flexrilog import GraphGenerator
sage: T = GraphGenerator.ThreePrismGraph()
sage: delta = T.NAC_colorings()[0]
sage: delta.is_singleton()
True

sage: Q1 = GraphGenerator.Q1Graph()
sage: [[(delta.name(), delta.is_singleton()) for delta in equiv_cls] for equiv_cls in Q1.NAC_colorings_isomorphism_classes()]
[[('psi2', False), ('psi1', False)],
 [('eta', True)],
 [('gamma1', True), ('gamma2', True)],
 [('phi4', False), ('phi3', False)],
 [('epsilon24', True),
  ('epsilon13', True),
  ('epsilon23', True),
  ('epsilon14', True)],
 [('zeta', False)]]

sage: delta = Q1.name2NAC_coloring('psi1')
sage: delta.is_singleton([Q1.name2NAC_coloring(name) for name in ['epsilon23', 'epsilon24', 'epsilon13', 'epsilon14']])
True

isomorphic_NAC_coloring(sigma, onlySets=False)

Return the NAC-coloring under a morphism sigma.

name()

Return the name of the NAC-coloring.

path_is_unicolor(path)

Return if the edges of the path have the same color.

plot(grid_pos=False, zigzag=False, **args_kwd)

Return a plot of the NAC-coloring.

EXAMPLES:

sage: from flexrilog import FlexRiGraph
sage: G = FlexRiGraph(graphs.CompleteBipartiteGraph(3,3))
sage: delta = G.NAC_colorings()[0]
sage: delta.plot()
Graphics object consisting of 16 graphics primitives

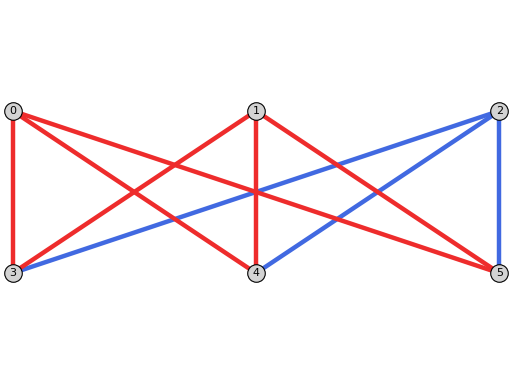
sage: from flexrilog import GraphGenerator
sage: G = GraphGenerator.ThreePrismGraph()
sage: delta = G.NAC_colorings()[0].conjugated()
sage: delta.plot(grid_pos=True)
Graphics object consisting of 16 graphics primitives

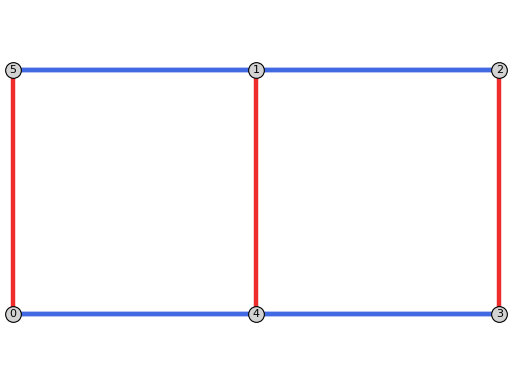
sage: from flexrilog import GraphGenerator
sage: G = GraphGenerator.ThreePrismGraph()
sage: delta = G.NAC_colorings()[0].conjugated()
sage: delta.plot(grid_pos=True, zigzag=True)
Graphics object consisting of 16 graphics primitives

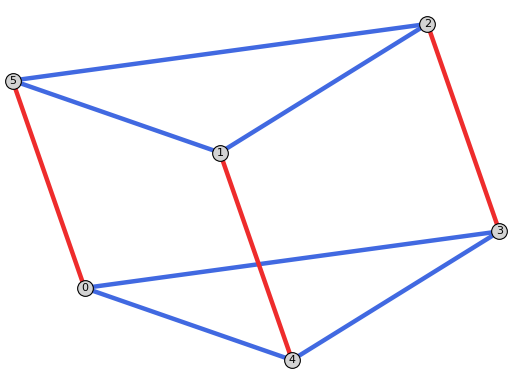
sage: from flexrilog import GraphGenerator
sage: G = GraphGenerator.ThreePrismGraph()
sage: delta = G.NAC_colorings()[0].conjugated()
sage: delta.plot(grid_pos=True, zigzag=[[[0,0], [0,1]], [[0,0], [1,1/2], [2,0]]])
Graphics object consisting of 16 graphics primitives

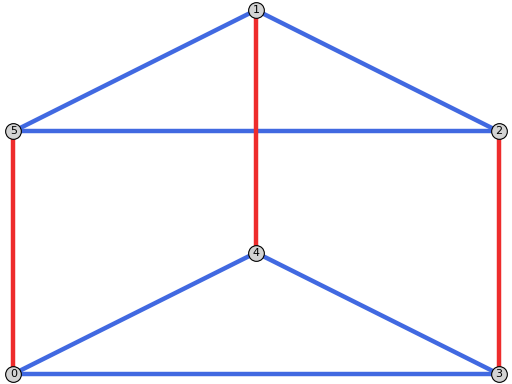
TODO:

doc

print_tikz()

Print TikZ code for the graph colored with the NAC-coloring.

red_components()

red_edges()

Return the list of red edges of the NAC-coloring.

red_subgraph()

set_name(new_name)

Set a new name.

EXAMPLES:

sage: from flexrilog import GraphGenerator
sage: G = GraphGenerator.SmallestFlexibleLamanGraph()
sage: delta = G.NAC_colorings()[0]; delta
NAC-coloring with red edges [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3]] and blue edges [[2, 4], [3, 4]]
sage: delta.set_name('delta'); delta
delta: NAC-coloring with red edges [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3]] and blue edges [[2, 4], [3, 4]]
sage: latex(delta)
\delta: \left( \{\{ 0 , 1 \},\{ 0 , 2 \},\{ 0 , 3 \},\{ 1 , 2 \},\{ 1 , 3 \}\} \mapsto red; 
\{\{ 2 , 4 \},\{ 3 , 4 \}\} \mapsto blue\right)