Graph Generator¶
This module generates some graphs relevant for rigidity and flexibility.
Graphs¶
K23Graph() |
Return the graph $K_{2,3}$. |
K33Graph() |
Return the graph $K_{3,3}$. |
L1Graph() |
Alias for ThreePrismGraph(). |
LamanGraphs() |
Return the Laman graphs with n vertices. |
MaxEmbeddingsLamanGraph() |
Return the Laman graph with n vertices with the maximum number of complex embeddings. |
NoNACGraph() |
Return a graph without NAC-coloring. |
Q1Graph() |
Return the graph $Q_1$. |
Q2Graph() |
Return the graph $Q_2$. |
Q3Graph() |
Return the graph $Q_3$. |
Q4Graph() |
Return the graph $Q_4$. |
Q5Graph() |
Return the graph $Q_5$. |
Q6Graph() |
Return the graph $Q_6$. |
S1Graph() |
Return the graph $S_1$. |
S2Graph() |
Return the graph $S_2$. |
S3Graph() |
Return the graph $S_3$. |
S4Graph() |
Return the graph $S_4$. |
S5Graph() |
Return the graph $S_5$. |
SmallestFlexibleLamanGraph() |
Return the smallest Laman graph that has a flexible labeling. |
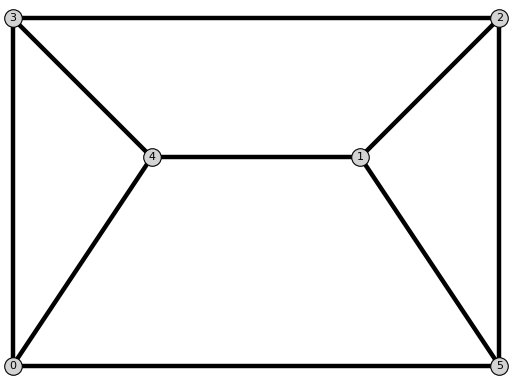
ThreePrismGraph() |
Return 3-prism graph. |
AUTHORS:
- Jan Legerský (2019-01-15): initial version
- Jan Legerský (2020-03-12): update to SageMath 9.0
TODO:
- L2, …, L6
- lists of L_i, Q_i, S_i graphs
-
class
flexrilog.graph_generator.GraphGenerator[source]¶ -
static
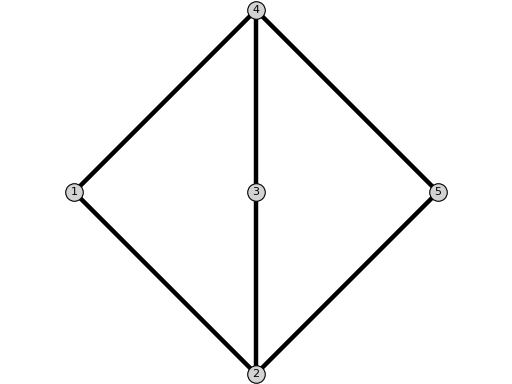
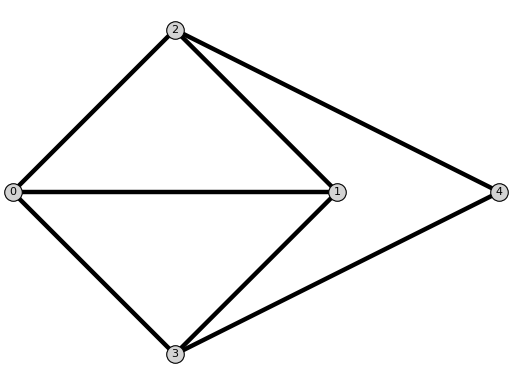
K23Graph()[source]¶ Return the graph $K_{2,3}$.
EXAMPLES:
sage: from flexrilog import GraphGenerator, FlexRiGraph sage: FlexRiGraph(graphs.CompleteBipartiteGraph(2,3)).is_isomorphic(GraphGenerator.K23Graph()) True
-
static
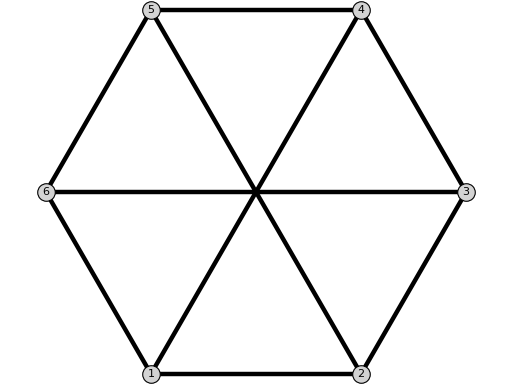
K33Graph()[source]¶ Return the graph $K_{3,3}$.
EXAMPLES:
sage: from flexrilog import GraphGenerator, FlexRiGraph sage: FlexRiGraph(graphs.CompleteBipartiteGraph(3,3)).is_isomorphic(GraphGenerator.K33Graph()) True
-
static
L1Graph()[source]¶ Alias for
ThreePrismGraph().
-
static
LamanGraphs(n)[source]¶ Return the Laman graphs with
nvertices.See [CGGKLS2018b].
INPUT:
nan integer from 3 to 8
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: [len(GraphGenerator.LamanGraphs(n)) for n in range(3,8)] [1, 1, 3, 13, 70] sage: GraphGenerator.ThreePrismGraph() in GraphGenerator.LamanGraphs(6) True
-
static
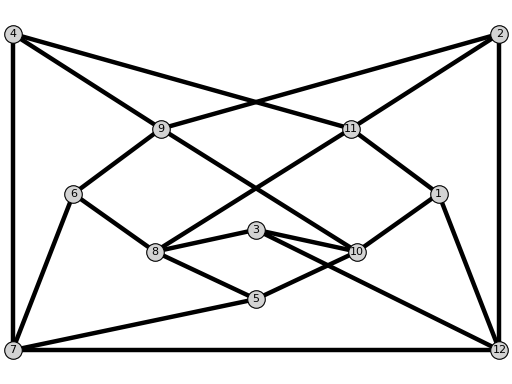
MaxEmbeddingsLamanGraph(n, labeled_from_one=True)[source]¶ Return the Laman graph with
nvertices with the maximum number of complex embeddings.See [GKT2018].
INPUT:
nan integer from 6 to 12
EXAMPLES:
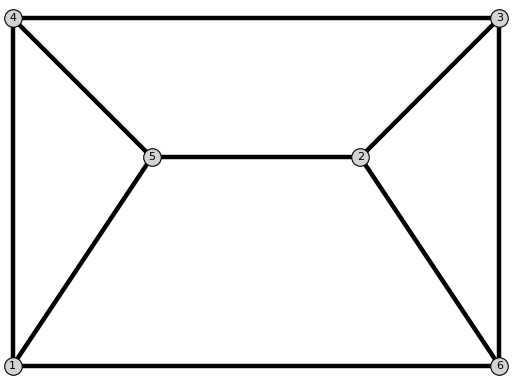
sage: from flexrilog import GraphGenerator sage: GraphGenerator.MaxEmbeddingsLamanGraph(6).is_isomorphic(GraphGenerator.ThreePrismGraph()) True
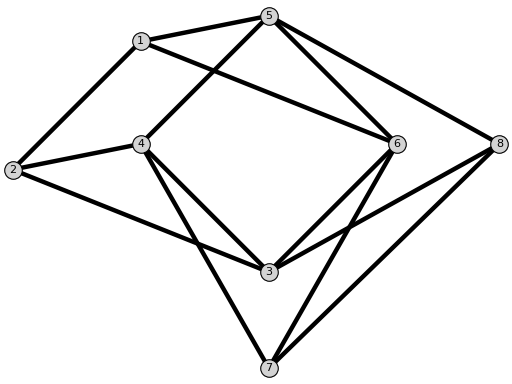
The graphs:
-
static
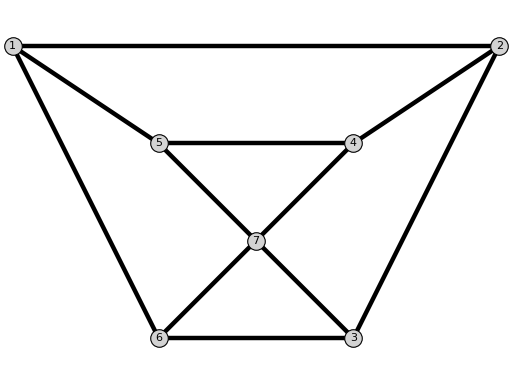
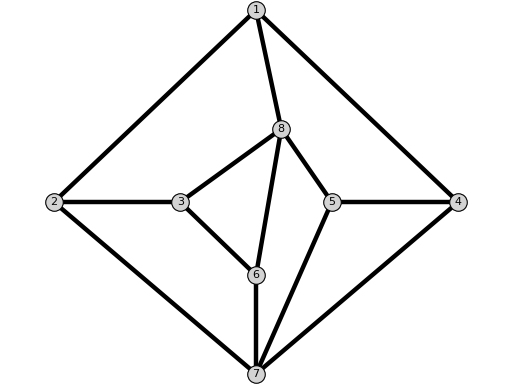
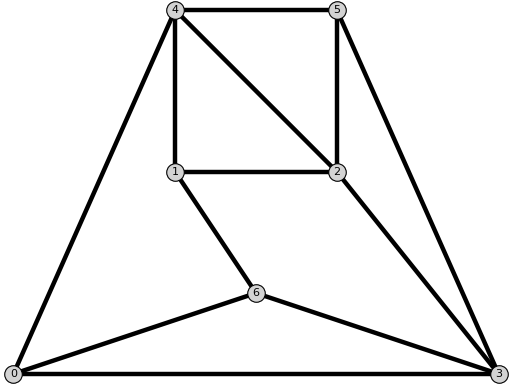
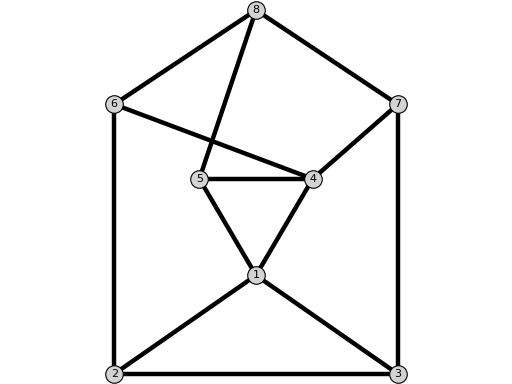
NoNACGraph()[source]¶ Return a graph without NAC-coloring.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.NoNACGraph() NoNAC: FlexRiGraph with 7 vertices and 12 edges
-
static
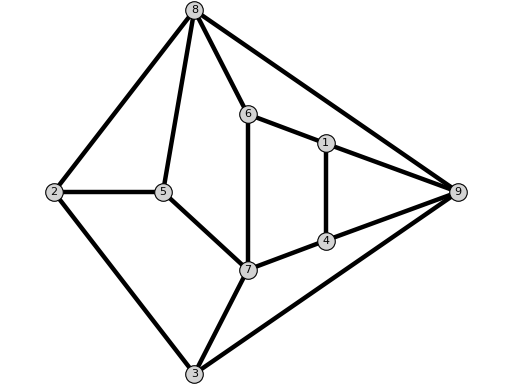
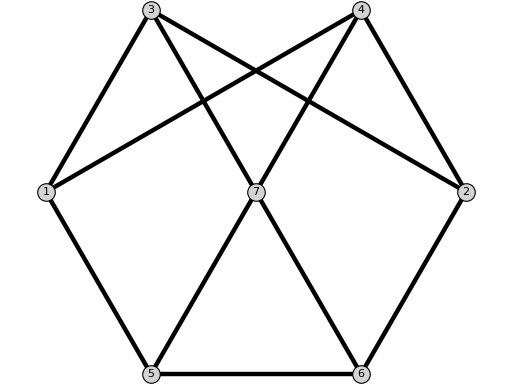
Q1Graph(old_labeling=False)[source]¶ Return the graph $Q_1$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.Q1Graph() Q_1: FlexRiGraph with 7 vertices and 11 edges
-
static
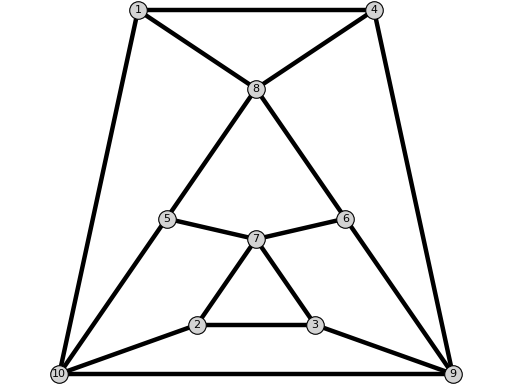
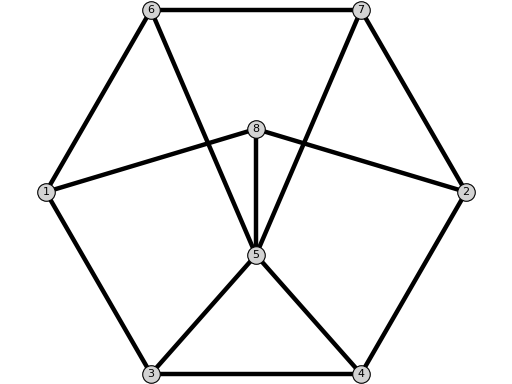
Q2Graph(old_labeling=False)[source]¶ Return the graph $Q_2$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.Q2Graph() Q_2: FlexRiGraph with 8 vertices and 13 edges
-
static
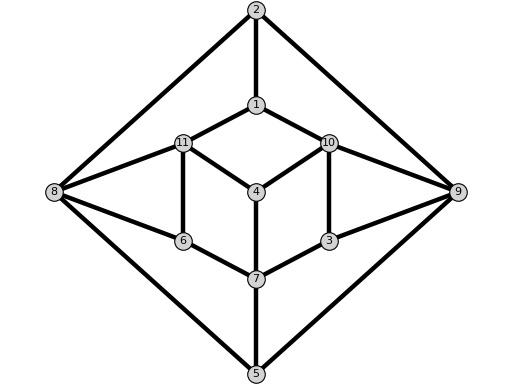
Q3Graph()[source]¶ Return the graph $Q_3$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.Q3Graph() Q_3: FlexRiGraph with 8 vertices and 14 edges
-
static
Q4Graph()[source]¶ Return the graph $Q_4$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.Q4Graph() Q_4: FlexRiGraph with 8 vertices and 14 edges
-
static
Q5Graph()[source]¶ Return the graph $Q_5$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.Q5Graph() Q_5: FlexRiGraph with 8 vertices and 13 edges
-
static
Q6Graph()[source]¶ Return the graph $Q_6$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.Q6Graph() Q_6: FlexRiGraph with 8 vertices and 13 edges
-
static
S1Graph()[source]¶ Return the graph $S_1$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.S1Graph() S_1: FlexRiGraph with 8 vertices and 14 edges
-
static
S2Graph()[source]¶ Return the graph $S_2$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.S2Graph() S_2: FlexRiGraph with 8 vertices and 14 edges
-
static
S3Graph()[source]¶ Return the graph $S_3$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.S3Graph() S_3: FlexRiGraph with 8 vertices and 14 edges
-
static
S4Graph()[source]¶ Return the graph $S_4$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.S4Graph() S_4: FlexRiGraph with 8 vertices and 14 edges
-
static
S5Graph(old_labeling=False)[source]¶ Return the graph $S_5$.
EXAMPLE:
sage: from flexrilog import GraphGenerator sage: GraphGenerator.S5Graph() S_5: FlexRiGraph with 8 vertices and 13 edges
-
static